深眸分享--手眼标定之眼在手外(基于opencv)
2022-05-24
在手眼系统的坐标系理论变换中,从像素坐标到机器人坐标系转换过程中需要经过内参矫正、外参矩阵平移旋转的变换。本章节将进一步讨论手眼系统在标定过程中的应用,如何通过opencv来求解我们需要的内参、外参矩阵参数。
opencv是一个开源的计算机视觉库,封装了很多相机标定所需要用到的算法,因此使用opencv来进行标定将能够极大简化手眼标定的步骤。我们将从代码层面简单剖析手眼标定的步骤以及注意事项。
在眼在手外Eye to Hand安装方式的手眼系统中,标定求解的是相机坐标系到机械臂末端夹具坐标系的变换关系
1.像素坐标畸变矫正
2.像素坐标转换为相机坐标并计算相机坐标与机械臂末端夹具坐标的变换关系
第一步就是我们常说的相机内参标定,第二步就是相机外参标定。通过opencv提供的一些坐标变换函数就可以实现眼在手外Eye to Hand标定过程。
以下讨论基于opencv 4.2.0版本,python语言环境。
这一步骤其实就是相机的内参计算,opencv提供以下关键函数:
cv2.findChessboardCorners(gray, (4, 7), None)
函数说明:在棋盘格图片中找到棋盘格内角点,内角点顺序由红色到紫色
cv2.cornerSubPix(gray, corners, (5, 5), (-1, -1), criteria)
函数说明:寻找亚像素内角点,为了得到更精确的像素坐标
cv2.calibrateCamera(obj_points, img_points, size, None, None)
函数说明:计算内参矩阵,该函数求解的内参矩阵是带畸变的。
注:用前三个方法就能够初步求解内参矩阵了,内参矩阵的结果有好有坏,取决于拍摄的标定板照片的数量以及标定在图片中的位置。标定图片的质量决定最终标定结果的精度,在内参标定过程中,需满足以下条件(以棋盘格为例):
标定图片所有的摆放位置要覆盖整个视场,以图像中心为原点分为四个象限,标定板位置分布在图像四个象限中,标定板占满图像1/4,
每个象限包含平放、两个不同方向的倾斜,一个象限拍摄3张图片。在中间区域拍摄平放、两个方向倾斜,总共拍摄标定图片15张。
满足光源条件,标定板图片清晰
标定过程中,相机的光圈,焦距不能改变,改变需要重新拍摄、标定
cv2. getOptimalNewCameraMatrix(mtx,dist,(w,h),alpha,(w,h))
函数说明:从内参/畸变系数中得到inner和outer矩阵,当alpha为0时,取inner即内矩阵,用内矩阵对应的尺寸作为新的图像大小,图像保留未失真像素,失真像素将被去掉,重新得到x、y方向的像素焦距fx、fy以及像素中心点cx、cy,即为无畸变内参矩阵。当alpha为1时,取outer即外矩阵,图像保留所有像素,同时填充0值像素点补充畸变矫正后多出来的部分。当alpha介于0~1时,则按照比例重新计算fx,fy,cx,cy。

cv2.undistort(img,mtx,dist,None,None)
函数说明:对图像进行畸变矫正,返回矫正的图像,用于检查计算得到的畸变系数的矫正效果。
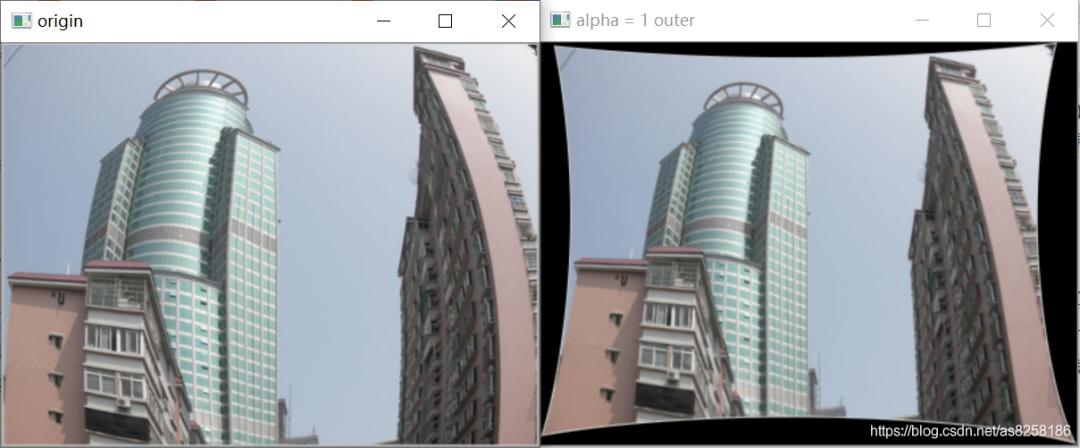
该函数第五个参数是无畸变内参,默认为空值,传参为outer内参矩阵时,矫正的结果为四周带黑边的图像,保留原畸变图像所有像素,如下图:

cv2.solvePnP(obj_coordinate,img_coordinate,mtx,dist)
函数说明:通过机器人坐标、像素坐标,以及前面函数求解得到的内参矩阵,畸变系数,来求解外参旋转矩阵、平移矩阵。
从solvePnP函数源码的逻辑中,可以分为两步:
第一步:输入的像素坐标经过undistortPoints转换为无畸变的图像坐标,此时图像坐标已畸变矫正,可应用小孔成像模型进行线性计算。
第二步:cvFindHomography函数求解图像坐标到机器人坐标的映射关系(旋转、平移)
上面描述的图像坐标,实际上是Zc=0的相机坐标,因为图像坐标是二维的,只有转换成三维的才能和机器人坐标三维关系对应上。
RT旋转平移向量的求解是和图像坐标直接相关,在求解RT矩阵的时候都需要确保图像坐标是无畸变的,而solvePnP函数内部调用了UndistortPoints函数进行畸变矫正求解无畸变图像坐标,因此,我们在使用solvePnP函数的时候也就存在两种方式:
方式一:传入畸变像素坐标、畸变内参mtx和畸变系数dist
这种方式是利用solvePnP内的UndistortPoints函数进行畸变矫正得到无畸变图像坐标
方式二:传入outer内参矩阵矫正后的像素坐标、outer内参矩阵,不传畸变系数dist
这种方式我们在调用solvePnP前就对像素坐标进行了矫正,并且传入的是outer内参矩阵,outer内参矩阵本身就已经包含了畸变矫正的结果,因此直接用矫正后的像素坐标和outer内参矩阵就能够计算得到无畸变的图像坐标。而不传畸变系数,就是直接跳过了solvePnP内的UndistortPoints函数计算,相当于solvePnP用外部的矫正结果来进行RT求解。
所以,我们在使用solvePnP时求解RT时满足上述两种方式的坐标、内参矩阵、畸变系数的对应关系即可,感兴趣的小伙伴可以查阅solvePnP源码。
R = cv2.Rodrigues(rvecs)[0]
函数说明:将solvePnP计算结果3x1旋转向量转换为3x3旋转矩阵的形式
以上就是在求解Eye to Hand手眼标定过程中,opencv所使用到的主要函数。那么,在得到旋转矩阵和平移矩阵后,如何计算机器人坐标系?
前面我们已经分析了解了solvePnP的求解RT矩阵的逻辑,RT矩阵是基于无畸变图像坐标求解得到,计算顺序:
像素坐标 -> 无畸变图像坐标 -> 机器人坐标 -> RT矩阵
反过来:
像素坐标 -> 无畸变图像坐标 -> RT矩阵 -> 机器人坐标
所以计算的关键在图像坐标上,只要满足图像坐标是无畸变的即可。我们在前一节的坐标系理论公式变换中以及上述分析中,计算机器人坐标的公式中需要用到像素坐标和相机内参,但是在opencv函数计算下存在这两个结果:畸变内参和outer无畸变内参。因此我们要计算无畸变图像坐标时,就有两种选择:
畸变像素坐标 + 畸变内参矩阵
无畸变像素坐标 + outer无畸变内参矩阵
然后按照前一节公式计算即可。
当然,在代码层面,我们也可以让求解机器人坐标的过程和求解RT外参的过程对应,在公式计算时,先用undistortPoints先算出图像坐标,再代入公式参与计算。
计算公式变为:

https://github.com/JayaoLiu/eye_to_hand_calibrate.git
前面分析求解RT矩阵时传参有两种方式,对应的, 用图像坐标求解机器人坐标也有两种方式:
方式一:原畸变图像->取畸变像素坐标->undistortPoints()矫正->无畸变图像坐标->RT计算->机器人坐标
方式二:原畸变图像->initRinitUndistortRectifyMap()/remap()图像矫正->取矫正图像的像素坐标->outer内参矩阵转换->无畸变图像坐标-> RT 计算 ->机器人坐标
方式一在视觉应用时,基于原畸变图像识别,识别畸变像素坐标产生的误差记为d1,undistortPoints()函数矫正时,像素坐标转图像坐标内参计算产生的误差记为d2,畸变矫正产生的误差记为d3,RT计算产生的误差记为d4,总的误差记为d = d1 + d2 + d3 + d4
方式二在视觉应用时,基于矫正后的图像识别,识别矫正图像的像素坐标产生的误差记为d1,像素坐标转图像坐标内参计算产生的误差记为d2,RT计算产生的误差记为d4,总的计算误差为d = d1 + d2 + d4。
所以,在视觉应用时,基于矫正图像进行识别后处理计算可以减少误差。总体来说,以上述方式标定后,机器人运行到图像指定位置的误差在5mm以内。
我们已经分析了在当我们已知像素坐标和机器人坐标,在眼在手外(Eye to Hand)的安装方式下,如何通过代码实现求解空间任意一点坐标的需求。像素坐标和机器人坐标的获取,以及获取坐标的精度,都会对后续的计算产生巨大的影响。到这里我们只描述了眼在手外的工程应用的问题,后续我们将继续讨论,眼在手上(Eye in Hand)安装方式下,如何完成标定以及工程应用。
